• Construction Knowledge Home
• Construction Knowledge Database
• Ned's Blog
• Best Phone Apps
• Our Construction Phone Apps
• About Us

CONSTRUCTION KNOWLEDGE  >> GENERAL TECHNICAL KNOWLEDGE >>

BASIC MATH
 

1. How do I change Inches to Decimal Feet and Avoid Errors?
2. What are the Basic Area and Volume Formulas?
3. Why Converting Units will be One of the Most Useful Things You will Ever Learn?
4. How do I Learn the Basics of Math and Algebra?
5. How do I Know When to Fold-'em in Texas Hold-'em?
6. What are 3 Useful Trigonometry Concepts?
7. Tricks of the Trade & Rules of Thumb for Basic Math:

How do I change Inches to Decimal Feet and Avoid Errors?

Bud Caldwell, one of the best Superintendents I ever worked with, taught me the value of changing inches into decimal feet. We were reviewing a shop drawing for a piece of equipment with lots of anchor bolts, and everything was in feet, inches and fractions of an inch. In his head, he quickly converted the inches and fractions of an inch into decimal feet, so we could easily add and check dimensions. He showed me a wonderful little trick of the trade that I've used for over 25 years. The inches to decimal feet conversion table shows illustrates the information.

As you know, adding fractions challenges most of us. We probably learned the concept of lowest common denominator at some point, but struggle to remember how to actually use it. So to add feet and inches, we have to deal with fractions and with that 12" in a foot concept, which means we have to add by hand, using pencil and paper. Special calculators for adding feet, inches and fractions of inches are available, but they always seemed difficult to use for me. So adding a string of dimensions in feet, inches and fractions of an inch gets much easier if we can simply convert to decimal feet.

Numerous situations occur where these conversions help:

1. Checking a string of dimensions to verify they correctly add
2. Comparing elevations between a site drawing (normally in decimal feet) and an architectural drawing (often in feet and inches)
3. Laying out accessible ramps and accessibility routes

Let's use accessible route as an example. Say the building finished floor elevation is 401' - 6 1/4" and the grade at the parking space is 400.14'. The sidewalk between the parking space and the front door has a distance of 30'. Now you probably know that an accessible route has a maximum slope of 5%, or it becomes a ramp and needs handrails. So 401' - 6 1/4" converts to 401.52. Then subtract 400.14 to find the grade change of 1.38'. To find the slope, divide the grade change of 1.38' by the distance of 30' to get a slope of .046 or 4.6%, which is less than the maximum of 5% allowed by code. So it works.

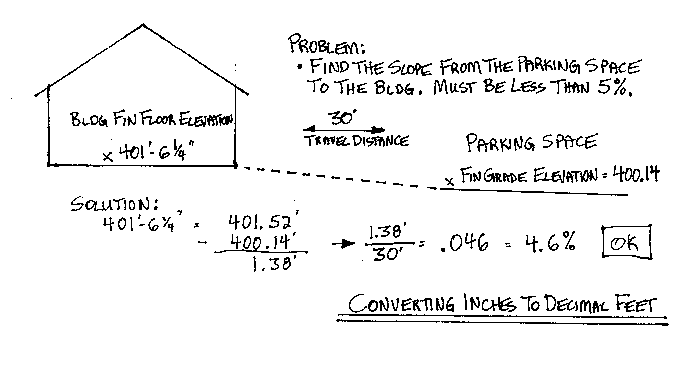
What are the Basic Area and Volume Formulas?

To figure how much concrete to order for a slab on grade, you need to know some basic area and volume formulas. Most of us understand that length times the width times the thickness gives us the volume. We may need a bit more help, though, when the things aren't rectangular or other complexities arise. Let's start with an example and work through how to utilize the geometry of common shapes.

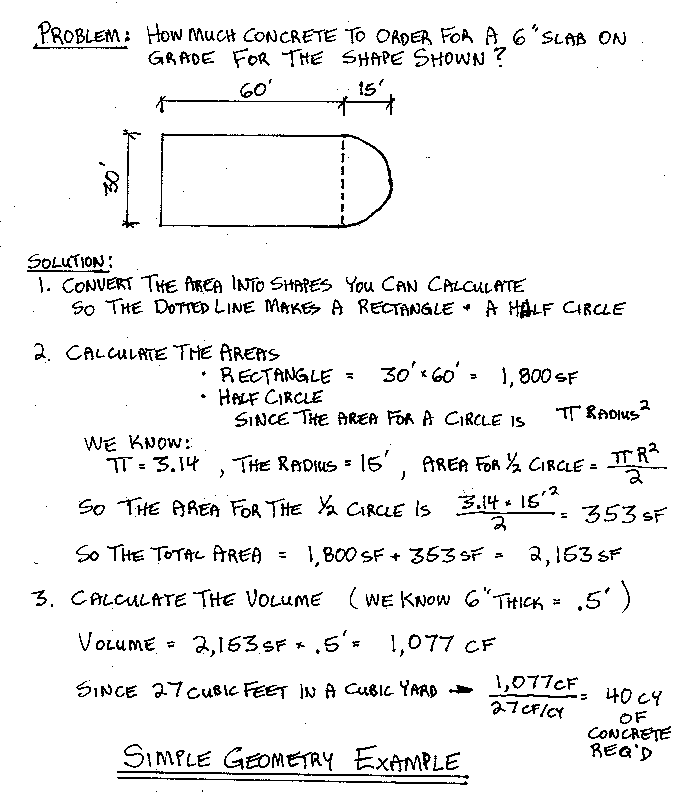
Hopefully, the example above makes sense to you and simply illustrates a few useful concepts. If you need some help understanding the example, you may want to review the US Navy Basic Math and Algebra training class. This course give lots of basic and more advanced information for understanding math.

The areas and volumes of common geometric shapes probably don't need to be memorized. It's usually simple just to know where to easily find the formulas. By knowing how to use these formulas, you will be able to solve many construction problems, such as:

1. How much soil needs to be moved? How many truckloads will actually be hauled? How many trucks are needed on site?
2. How much concrete to order for the pour?
3. How much does something weigh? What will it take to lift it?
4. How much water will be in that pool? How long will it take to fill it?

These questions and many more get solved by knowing how to calculate the areas and volumes of Common Geometric Shapes.

Why Converting Units will be One of the Most Useful Things You Will Ever Learn?

I remember learning how to convert units in Biology Class in high school. I've used that skill ever since that time and it has helped me solve many problems (and avoid lots of mistakes). The process of converting units is simple and powerful. The secret to consistently getting the right answers lies in always listing the units and taking the time to cancel the units as you proceed through the process. A few examples shown below in "Converting Units - Examples" which illustrates the process clearly.

By learning to solve problems by setting up simple math problems, you will be amazed at how many complicated issues you can understand and problems you can solve. The problem solver with a good attitude advances, making more money and getting more responsibility. So take the time to learn how to set up simple math problems that help you convert units. Use this same technique every time:

1. Always write the problem down.
2. Always list the units (even if it seems simple to you)
3. Always go through and cancel the units to make sure the answer you get is in the correct units

This simple little technique can really help you.

How do I Learn the Basics of Math and Algebra?

The ability to use math as a tool can separate you from many others in the construction field. Just as carpenters work at a level above laborers partly because of their skill with tools, you can work at a higher level with the ability to formulate and solve number problems.

The US Navy Basic Math and Algebra course provides instruction that assumes no prior knowledge. You can use this course in one of two ways:

1. Work through the entire course from start to finish and gain a firm understanding of the fundamentals.
2. Focus on an area you need to understand right now (perhaps percentages aren't clear to you or how to solve problems with fractions or maybe you need a review of simple algebra to know how to find the unknown quantity in a situation).

The advantage of working through the entire course comes from the fact that math knowledge builds on itself. The more clearly you understand the basic building blocks of math, the better you will learn and retain more advanced concepts. The disadvantage of working through the entire course is the time it will take and that you will probably learn many things that aren't directly applicable to construction.
 

How do I Know When to Fold-'em in Texas Hold-'em?

You don't really need to know anything about Probability and Statistics for construction (at least I don't think you do). So why do I include the US Navy Probability and Statistics courses? It's cool stuff to know.

Understanding basic probability theory helps you understand life. To have a basic grasp of how random events happen will allow you to better assess risks and rewards. And it helps your poker game! You can check out some teaching about probability at the US Navy Pre-Calculus and Probability course.

Statistics, on the other hand, is the math that helps you understand large bunches of information. We use statistics to help us make informed decisions. A construction company, as an example, may be concerned with improving productivity for its trades people. As various bits of information is analyzed, perhaps they find that the absenteeism on Fridays is significantly higher than any other day. Statistics can be used to help understand how much of that absenteeism is just random or if it's a significant finding. Say the statistics indicate a substantially higher absenteeism on Fridays, then the company looks for causes. The employees get their paychecks on Thursday afternoons. So now there is a management choice to be made.

Many construction companies use quality improvement programs that utilize statistics. If a company wants to improve results, they must understand what's really going on in their day to day processes. To understand how processes are truly working, we need to measure things, then try to figure out what is significant. Statistics help us understand what is really going on. Some good teaching on statistics can be found in the US Navy Introduction to Statistics course. 
 

What are 3 Useful Trigonometry Concepts?

When most people hear "Trigonometry", they they assume it's something they could never understand nor use. I've actually never had a course on trigonometry, so I'm no expert, but I learned three really useful things on my own. Sine, Cosine and Tangent help me solve all sorts of problems. If I'm actively involved in building anything, I'm using these few simple formulas. The figure below explains the concepts and gives some examples.

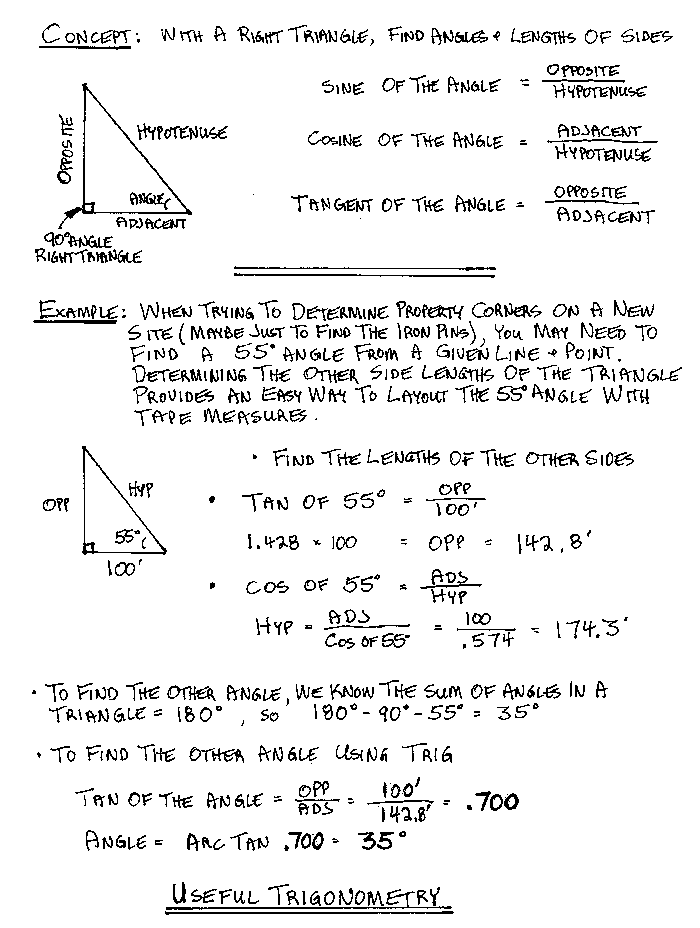
If you want some more information on trigonometry, see the US Navy Trigonometry course.
 

Tricks of the Trade & Rules of Thumb for Basic Math:

1. Convert feet, inches and fractions of an inch to decimal feet to easily add, subtract and multiply.
2. When converting units, always write the units and cancel them as you proceed through the conversion.
3. Use sine, cosine and tangent to determine angles and side lengths in right triangles (useful trigonometry).